W.B.C.S. Notes On – Physics – Spherical Lenses.

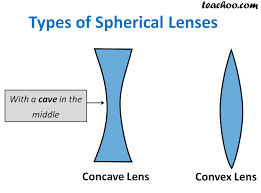
• A transparent material (normally glass) bound by two surfaces, of which one or both surfaces are spherical, is known as “spherical lens.”Continue Reading W.B.C.S. Notes On – Physics – Spherical Lenses.

Convex Lens

• A lens may have two spherical surfaces, bulging outwards (as shown in the image given below), is known as convex lens or a double convex lens.

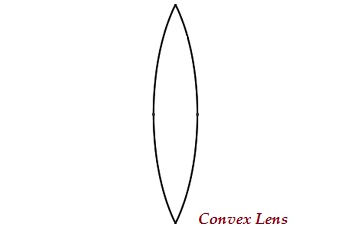
• The middle part of this lens is bulged (thicker) and at the both ends, it is narrow.
• Convex lens converges the light rays; therefore, it is also known as converging lens.

Concave Lens

• A lens may have two spherical surfaces, curved inwards (as shown in the image given below), is known as concave lens or a double concave lens.

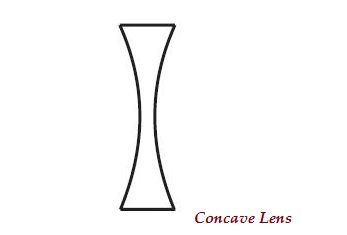
• The middle part of this lens is narrow (curved inwards) and the both the edges are thicker.
• Concave lens diverges the light rays; therefore, it is also known as diverging lens.
• A lens, either a concave or a convex, has two spherical surfaces and each of these surfaces forms a part of the sphere. The centers of these spheres are known as centers of curvature, represented by English letter ‘C.’
• As there are two centers of curvature, therefore, represented as ‘C₁’ and ‘C₂.’
• An imaginary straight line, passing through both the centers of curvature of a lens, is known as principal axis.
• Optical center is the central point of a lens. It is represented by ‘O.’
• An aperture is the actual diameter of the circular outline of a spherical lens.
• Principal focus of lens is represented by ‘F.’
• A lens has usually two foci represented as F₁ and F₂.
• Focal length is the distance between the principal focus and the optical center of a lens. It is represented by ‘f.’
• The following table illustrates, the nature and position of images formed by a convex lens −

Position of Object	Position of Image	Size of Image	Nature of Image	Image
At infinity	At the focus F2	Highly diminished, pointsized	Real and inverted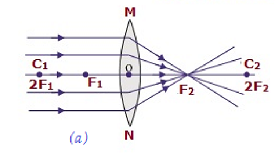
Beyond 2F1	B/w F2 and 2F2	Diminished	Real and inverted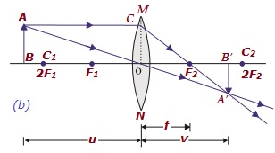
At 2F1	At 2F2	Same size	Real and inverted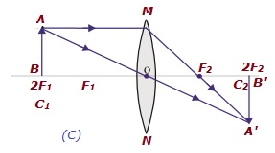
B/w F1 & 2F1	Beyond 2F2	Enlarged	Real and inverted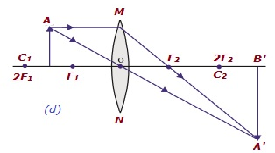
At focus F1	At infinity	Infinitely large or highly enlarged	Real & inverte d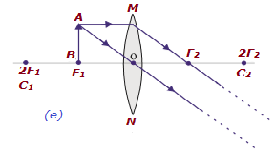
B/w focus F1& optical center O	On the same side of the lens as the object	Enlarged	Virtual and erect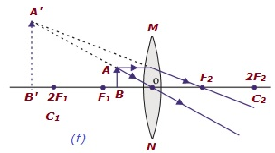

• The following table illustrates, the nature and position of images formed by a concave lens −

Position of Object	Position of Image	Relative Size of Image	Nature of Image	Image
At infinity	At the focus F1	Highly diminishe d, pointsized	Virtual and erect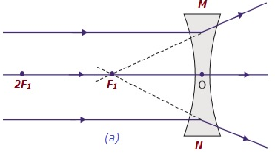
B/w infinity & optical center O of the lens	B/w F1 & optical center O	Diminishe d	Virtual and erect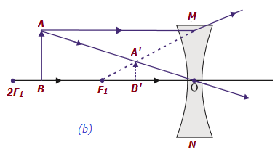

Lens Formula

• • The formula is expressed as −

• Lens formula expresses the relationships among the object-distance (i.e. u), image-distance (i.e. v), and focal length (i.e. f) of a lens.

Our own publications are available at our webstore (click here).

For Guidance of WBCS (Exe.) Etc. Preliminary , Main Exam and Interview, Study Mat, Mock Test, Guided by WBCS Gr A Officers , Online and Classroom, Call 9674493673, or mail us at – mailus@wbcsmadeeasy.in
Visit our you tube channel WBCSMadeEasy™ You tube Channel
Please subscribe here to get all future updates on this post/page/category/website