Weak Law Of Large Numbers – Statistics Notes – For W.B.C.S. Examination.

বৃহৎ সংখ্যার দুর্বল আইন – স্ট্যাটিসটিক্স নোট – WBCS পরীক্ষা।

The Weak Law of Large Numbers, also known as Bernoulli’s theorem, states that if you have a sample of independent and identically distributed random variables, as the sample size grows larger, the sample mean will tend toward the population mean.Continue Reading Weak Law Of Large Numbers – Statistics Notes – For W.B.C.S. Examination.

To put this in formal mathematical notation, it looks like this:

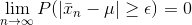
We can prove this using Chebyshev’s inequality, which says the probability that a random variable X differs from its mean by some small constant k is less than or equal to the variance of X divided by the the square of the constant k.

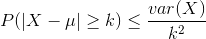
Since the random variable X and the constant k can be anything, we can replace X with the sample mean and replace k with epsilon.

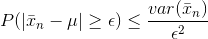
Because we assumed that our sample contains independent and identically distributed random variables, we can simplify the right side of the equation.

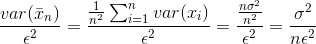
Replacing the right side of Chebyshev’s inequality, we have the following.

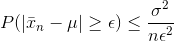
As n tends to infinity, it follows that the right side of the inequality equals 0.

Our own publications are available at our webstore (click here).

For Guidance of WBCS (Exe.) Etc. Preliminary , Main Exam and Interview, Study Mat, Mock Test, Guided by WBCS Gr A Officers , Online and Classroom, Call 9674493673, or mail us at – mailus@wbcsmadeeasy.in
Visit our you tube channel WBCSMadeEasy™ You tube Channel
Please subscribe here to get all future updates on this post/page/category/website