Cube – Logical Reasoning – For W.B.C.S. Examination.

কিউব – যৌক্তিক যুক্তি – WBCS পরীক্ষা।

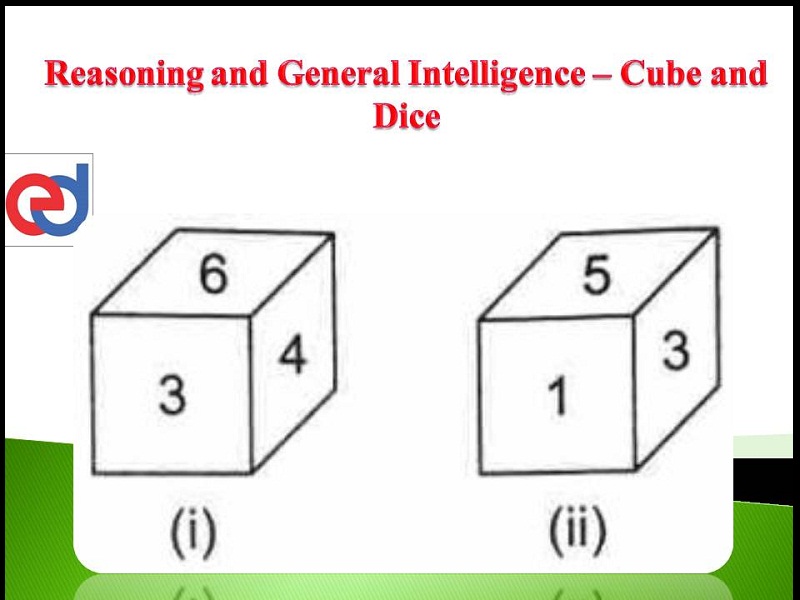
Cubes is one of the most frequently asked puzzle topics in W.B.C.S Examination. These puzzles require us to think visually about the puzzle, which makes it somewhat tougher than other type of puzzles. We will discuss the basic concepts of the cube and few things that we would be using is majority of the puzzles related to cubes. Cube related puzzles are asked in a number of ways unlike selection or arrangement puzzles, where the primary pattern remains the same.Continue Reading Cube – Logical Reasoning – For W.B.C.S. Examination.

Few things to remember while dealing with a cube:

• A cube has 6 faces
• A cube has 12 edges
• A cube has 8 vertices

Let us make a cut parallel to the base of the cube. We get two solids. If we make another cut parallel to the base, we get three solids. For n cuts mutually parallel to the base (or any other face), we get n+1 solid pieces. 

If we make one cut parallel to the base (say x-axis) and another cut perpendicular to the first cut (say y axis), the second cut will divide each of the two solids we get from the first cut into two pieces. We get total 4 pieces or 4 parts of the initial big cube. Similarly, another cut parallel to both the previous cuts (z-axis) will further divide these 4 pieces into two pieces each, thus making the total pieces as 8. When we analyze this, we see that when we make X mutually parallel cuts along x-axis, Y mutually parallel  cuts along y axis and Z mutually paralel cuts along z axis we get (X+1)*(Y+1)*(Z+1) pieces of the original cube. X cuts along x itself will produce X+1 pieces and when we cut each of those pieces with Y cuts, each of them will produce Y+1 pieces and similar with Z cuts.

Note that, all the pieces will not necessarily be cubes. They can be cubes or cuboids. All the pieces are cubes when X = Y = Z and all the cuts are equidistant.This is the scenario when the number of cuts are given to us. Sometimes, we are given the sum of X + Y + Z instead of individual values.

MINIMUM NUMBER OF PIECES WITH A GIVEN TOTAL NUMBER OF CUTS

When we are given total number of cuts, the cuts can be made in any axis. Say if we make total 12 cuts, all 12 can be in x-axis, or 6 in x and 6 in y-axis etc. For a given number of cuts, we can have a number of combinations. We get the minimum number of pieces when all the cuts are made in the same axis. If we make all 12 cuts along x-axis, total 13 pieces are formed. All other combinations will result in more than 13 pieces. Let’s say, 11 cuts along x-axis and 1 cut along y. The total number of pieces formed is (11+1)*(1+1) = 24.

MAXIMUM NUMBER OF PIECES WITH A GIVEN TOTAL NUMBER OF CUTS

In order to get maximum number of pieces with given number of cuts, divide the total cuts equally among the three axis. If we divide 12 cuts equally among the three axis, we get 4 cuts in each axis resulting in (4+1)*(4+1)*(4+1) = 125 pieces overall. But what if the total number of cuts cannot be divided equally among the three axis. For a number like 14, we cannot distribute equally among all thethree axis. In such case, to maximize the total number of pieces, we need to minimize the difference between the number of cuts in any two axis is minimum. For 14 cuts, we can divide it as X = 5, Y = 5, Z = 4. Any other combination of numbers will result in a lower number of pieces. If we analyze, we see that in case of equal cuts, the difference between the numbers of cuts is zero that results in the maximum number of pieces.

NUMBER OF CUTS FROM TOTAL NUMBER OF PIECES GIVEN

The question can also mention the total number of pieces formed after a certain number of cuts. We need to find the number of cuts in different axis based upon the requirement of the question. Suppose, a cube is cut into 10 pieces. Now 10 = (X+1)*(Y+1)*(Z+1). Now 10 is to be represented as the product of 3 numbers or factors. We can have, 10 = 1*1*10 or 1*2*5.

Minimum numbers of cuts is obtained if we factorize the number of pieces into three equal factors. If three equal factors are not possible, then we should minimize the difference between the numbers.In case of 10 pieces, 1*2*5 gives minimum difference between factors.

To maximize the total number of cuts, all the cuts are made in one axis. For instance, for 10 pieces, factors are 10*1*1 that means the x-axis cuts are 9 and no cut is made in other two axis.

For Guidance of WBCS (Exe.) Etc. Preliminary , Main Exam and Interview, Study Mat, Mock Test, Guided by WBCS Gr A Officers , Online and Classroom, Call 9674493673, or mail us at – mailus@wbcsmadeeasy.in
Visit our you tube channel WBCSMadeEasy™ You tube Channel
Please subscribe here to get all future updates on this post/page/category/website