Fundamental Theorem Of LPP – Mathematics Notes – For W.B.C.S. Examination.
We establish the validity of Theorem 1, through a series of observations:Continue Reading Fundamental Theorem Of LPP – Mathematics Notes – For W.B.C.S. Examination.
- First notice that according to the previous discussion, the feasible region of an LP is a polytope, and thus, convex.
- Furthermore, since we assume that the LP has an optimal solution, let
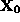 denote such an optimal point. The optimal objective value will be denoted by
denote such an optimal point. The optimal objective value will be denoted by  .
. - Then notice that point
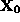 cannot be interior to a line segment that is not perpendicular to the direction of improvement to the “isoprofit” hyperplanes – w.l.o.g., let’s assume a maximization LP for our discussion – defined by vector
cannot be interior to a line segment that is not perpendicular to the direction of improvement to the “isoprofit” hyperplanes – w.l.o.g., let’s assume a maximization LP for our discussion – defined by vector  . Otherwise, by moving on this line segment in the direction of improvement of the “isoprofit” hyperplanes,we would be able to obtain another point
. Otherwise, by moving on this line segment in the direction of improvement of the “isoprofit” hyperplanes,we would be able to obtain another point  of the feasible region, such that
of the feasible region, such that  . But this contradicts the assumption that
. But this contradicts the assumption that 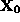 is an optimal point. Figure 9 depicts this argument.
is an optimal point. Figure 9 depicts this argument. 
Figure 9: Why an optimal solution to an LP cannot be interior to a line segment not perpendicular to the direction of improvement of the “isoprofit” hyperplanes - However, point
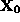 can be interior to a line segment of the feasible solution space which is perpendicular to the direction of improvement of the optimal “isoprofit” hyperplane. This, in fact, corresponds to a situation of many optimal solutions. In this case, notice that this line segment must have at least one end
can be interior to a line segment of the feasible solution space which is perpendicular to the direction of improvement of the optimal “isoprofit” hyperplane. This, in fact, corresponds to a situation of many optimal solutions. In this case, notice that this line segment must have at least one end  defined by the fact that one (or more) additional constraint is binding at this point. Otherwise, the problem is ill-posed, since we can vary some variable(s) at will over
defined by the fact that one (or more) additional constraint is binding at this point. Otherwise, the problem is ill-posed, since we can vary some variable(s) at will over  with this variation affecting neither the constraints nor the objective.
with this variation affecting neither the constraints nor the objective. - Hence,
 , being on the optimal “isoprofit” hyperplane, is another optimal point at which an additional constraint is binding. Then, there are two possibilities: (i)
, being on the optimal “isoprofit” hyperplane, is another optimal point at which an additional constraint is binding. Then, there are two possibilities: (i)  is an extreme point of the feasible region, in which case we are done, or (ii)
is an extreme point of the feasible region, in which case we are done, or (ii)  is interior point to another line segment lying in the optimal “isoprofit” hyperplane
is interior point to another line segment lying in the optimal “isoprofit” hyperplane  , which binds, however, an additional constraint, compared to point
, which binds, however, an additional constraint, compared to point 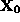 . In this case, repeating the argument above, we establish the existence of another end point
. In this case, repeating the argument above, we establish the existence of another end point  , determined by the binding of at least one more constraint. Then, we repeat the entire argument for
, determined by the binding of at least one more constraint. Then, we repeat the entire argument for  , and so on. Figure 10 depicts this part of the proof.
, and so on. Figure 10 depicts this part of the proof. 
Figure 10: Identifying an optimal extreme point on the optimal isoprofit hyperplane - Finally, notice that every time we bind an additional constraint, we restrict the (sub-)space of optimal solutions considered by one “degree of freedom”. Since an n-dim space has n “degrees of freedom”, the number of end points visited in the argument above before we find one that it is an extreme point is finite. Thus, this last observation establishes the existence of an optimal extreme point for the case of many optimal solutions, and the proof is complete.
The discourse of the previous proof has also revealed a very important property of extreme points: At these points, the number of binding constraints is such that it allows zero “degrees of freedom”, or, in other words, these constraints define the point uniquely. Starting from this observation, in the next section we provide a series of algebraic characterizations of the extreme points, which will eventually allow us to analytically manipulate the set of extreme points of an LP, in the context of the Simplex algorithm. As it has been previously mentioned, this algorithm exploits the result stated in the Fundamental Theorem above, by limiting the search for an optimal solution over the set of extreme points of the polytope defining the LP feasible region. In the next section, we shall show that this set is finite and discrete, so it can even be exhaustively enumerated. Simplex algorithm provides an efficient way to search this set.
For Guidance of WBCS (Exe.) Etc. Preliminary , Main Exam and Interview, Study Mat, Mock Test, Guided by WBCS Gr A Officers , Online and Classroom, Call 9674493673, or mail us at – mailus@wbcsmadeeasy.in
Visit our you tube channel WBCSMadeEasy™ You tube Channel
Please subscribe here to get all future updates on this post/page/category/website



 +919674493673
+919674493673  mailus@wbcsmadeeasy.in
mailus@wbcsmadeeasy.in