Lagrange’s Method Of Multipliers – Mathematics Notes – For W.B.C.S. Examination.
লাগরঞ্জের মাল্টিপ্লায়ার পদ্ধতি – গণিতের নোট – WBCS পরীক্ষা।
There are many rules regarding what optional subject to choose for the W.B.C.S. exam. A general rule of thumb is that you should take the subject in which you have some background and a genuine interest and practice till you are perfect.. In case you are a mathematics graduate and enjoy learning this subject, choosing maths as your W.B.C.S.optional might be a good idea. Mathematics is one of the most scoring optional in the W.B.C.S. Mains examination. The aspirants from B. Sc Mathematics or B. Tech background can take Mathematics as the optional in this examination. Learning Mathematics is always fun. Right strategy and thorough practice is the key to crack Mathematics optional.The method of Lagrange multipliers is a method for finding extreme of a function of several variables restricted to a given subset.Continue Reading Lagrange’s Method Of Multipliers – Mathematics Notes – For W.B.C.S. Examination.
Let us begin with an example. Find the maximum and minimum of the function z=f(x,y)=6x+8y subject to the constraint g(x,y)=x^2+y^2-1=0. We can solve this problem by parameterizing the circle and converting the problem to an optimization problem with one independent variable, that can be tackled using techniques from single variable calculus. In this section we apply the method of Lagrange multipliers instead.
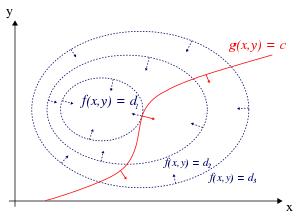
The key to understanding this technique is the following figure, which plots the constraint function and the level curves of f(x,y).

The constraint function is the circle of radius 1 centered at the origin. Recall that the level curves of f(x,y)=6x+8y are the curves defined by 6x+8y=C, where C is a constant. These curves are the straight lines in the figure . On 6x+8y=C, f(x,y)=C. The value of C is listed on each level curve in the figure. As the plot shows, the function of f(x,y) takes on values between -10 and 10 for points on the circle. Hence, the maximum is 10 and the minimum is -10.
Note that the maximum and minimum occur at points where the constraint curve is tangent to the level curve! There is another way to characterize the extreme points: the maximum and minimum occur at points where the normal to constraint curve and the normal to level curve point in the same direction! The vectors at the max and min in the figure above are the normal vectors.To view W.B.C.S. Mathematics Optional Syllabus , Click here.
As discussed previously, the gradient vector
![]()
is normal to the level curve of f through (x,y). It turns out that the normal vector to the constraint curve is the gradient of g:
![]()
Why is this last fact true? Let z=g(x,y). The constraint curve g(x,y)=0 is a level curve corresponding to 0. Hence, the gradient vector of g(x,y) on the constraint curve is normal to the constraint curve.
At the maximum and minimum points the normal vectors point in the same direction. That means that the normal vectors are multiples of each other:
![]()
Here the unknown multiplier
![]()
is called the Lagrange multiplier. For the case of functions of two variables, this last vector equation can be written:
![]()
For our problem
![]()
and
![]()
Hence, the above vector equation consists of the following 2 equations
![]()
and
![]()
These last 2 equations have 3 unknowns: x, y, and lambda. We need a third equation to solve for the 3 variables. The third equation is the constraint equation:
![]()
We now solve these last equations. Solving for x and y in the first two equations, we have:
![]()
Substituting these expressions for x and y in the constraint equation, we have:
![]()
Solving this last equation, we obtain lambda=+5 and lambda =-5. If lambda=5, then x=3/5 and y=4/5 and f(x,y)=10. This is maximum value of f(x,y). If lambda=-5, then x=-3/5 and y=-4/5 and f(x,y)=-10. This is the minimum value of f(x,y).
In general, the equations that must be solved simultaneously are nonlinear, and there is no simple recipe for solving them.
The Lagrange multiplier technique can be applied to problems in higher dimensions. Consider the problem: find the extreme values of w=f(x,y,z) subject to the constraint g(x,y,z)=0. In this case we get the following 4 equations for the 4 unknowns x, y, z, and lambda.
![]()
![]()
![]()
and the constraint equation:
![]()
For this problem, the constraint is a surface in xyz space.
Please subscribe here to get all future updates on this post/page/category/website


 +919674493673
+919674493673  mailus@wbcsmadeeasy.in
mailus@wbcsmadeeasy.in





































































































1 Comment
Please upload wbcs 2022 main Optional mathematics question paper as early as possible..