Mathematics Notes On – Polar Coordinates – For W.B.C.S. Examination.

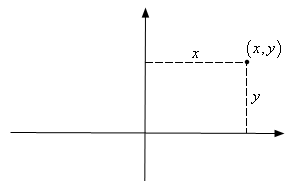
There are many rules regarding what optional subject to choose for the W.B.C.S.  exam. A general rule of thumb is that you should take the subject in which you have some background and a genuine interest and practice till you are perfect.. In case you are a mathematics graduate and enjoy learning this subject, choosing maths as your W.B.C.S.optional might be a good idea. Mathematics is one of the most scoring optional in the W.B.C.S. Mains examination. The aspirants from B. Sc Mathematics or B. Tech background can take Mathematics as the optional in this examination.  Learning Mathematics is always fun. Right strategy and thorough practice is the key to crack Mathematics optional.Coordinate systems are really nothing more than a way to define a point in space. For instance in the Cartesian coordinate system at point is given the coordinates $\left(x,y\right)$ and we use this to define the point by starting at the origin and then moving $x$ units horizontally followed by $y$ units vertically. This is shown in the sketch below.Continue Reading Mathematics Notes On – Polar Coordinates – For W.B.C.S. Examination.

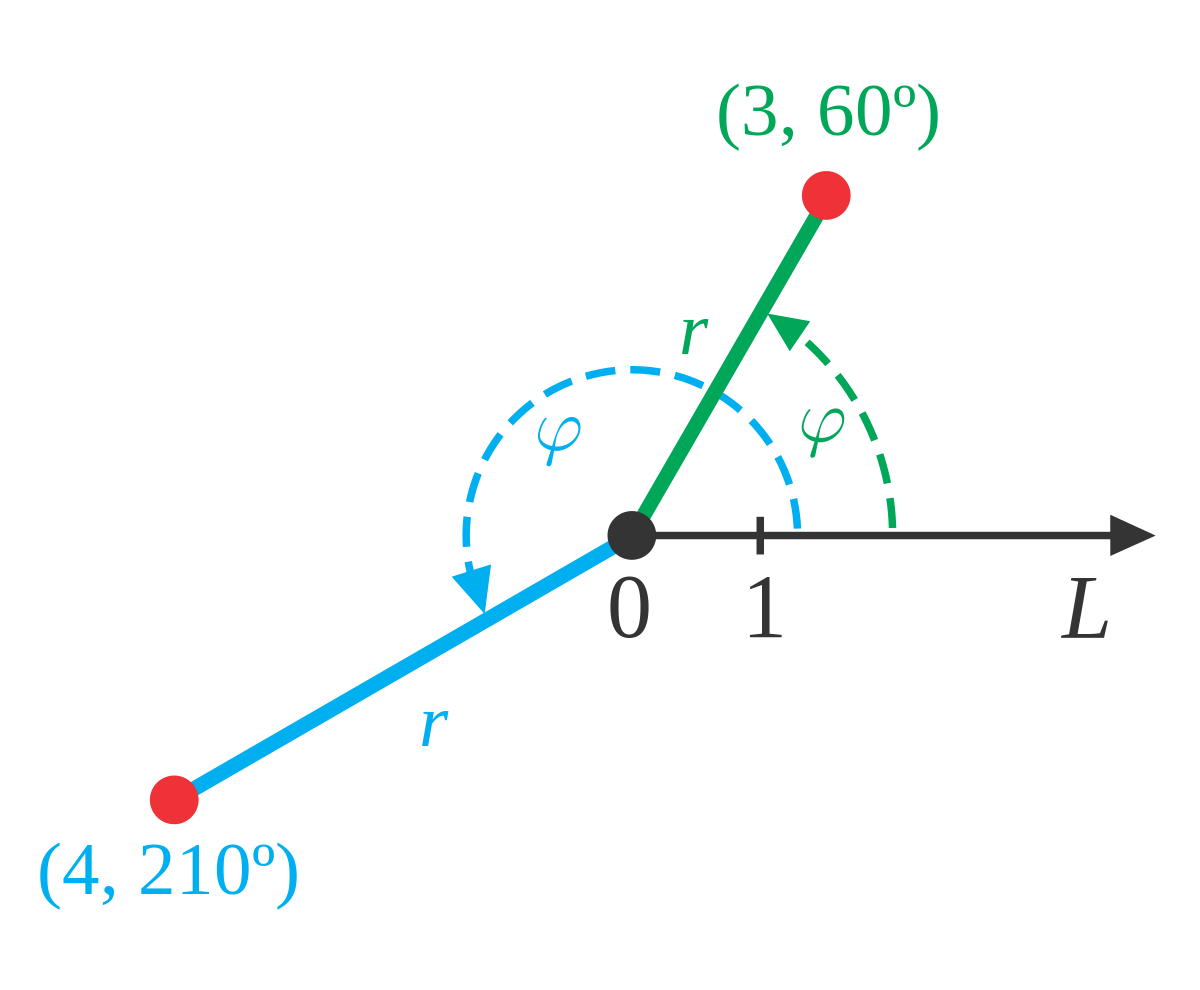
This is not, however, the only way to define a point in two dimensional space. Instead of moving vertically and horizontally from the origin to get to the point we could instead go straight out of the origin until we hit the point and then determine the angle this line makes with the positive $x$-axis. We could then use the distance of the point from the origin and the amount we needed to rotate from the positive $x$-axis as the coordinates of the point. This is shown in the sketch below.

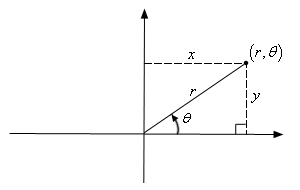
Coordinates in this form are called polar coordinates.

The above discussion may lead one to think that $r$ must be a positive number. However, we also allow $r$ to be negative. Below is a sketch of the two points $\left(2,\frac{\pi }{6}\right)$ and $\left(-2,\frac{\pi }{6}\right)$.

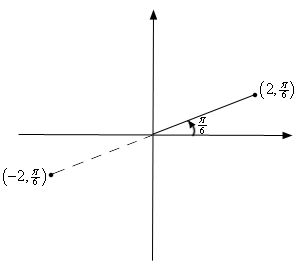
From this sketch we can see that if $r$ is positive the point will be in the same quadrant as $\theta$. On the other hand if $r$ is negative the point will end up in the quadrant exactly opposite $\theta$. Notice as well that the coordinates $\left(-2,\frac{\pi }{6}\right)$ describe the same point as the coordinates $\left(2,\frac{7\pi }{6}\right)$ do. The coordinates $\left(2,\frac{7\pi }{6}\right)$ tells us to rotate an angle of $\frac{7\pi }{6}$ from the positive $x$-axis, this would put us on the dashed line in the sketch above, and then move out a distance of 2.

This leads to an important difference between Cartesian coordinates and polar coordinates. In Cartesian coordinates there is exactly one set of coordinates for any given point. With polar coordinates this isn’t true. In polar coordinates there is literally an infinite number of coordinates for a given point. For instance, the following four points are all coordinates for the same point.

$$\left(5,\frac{\pi }{3}\right)=\left(5,-\frac{5\pi }{3}\right)=\left(-5,\frac{4\pi }{3}\right)=\left(-5,-\frac{2\pi }{3}\right)$$

Here is a sketch of the angles used in these four sets of coordinates.

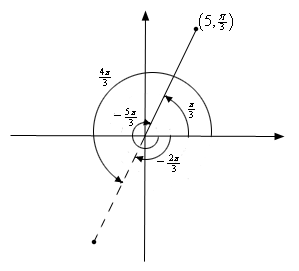
In the second coordinate pair we rotated in a clock-wise direction to get to the point. We shouldn’t forget about rotating in the clock-wise direction. Sometimes it’s what we have to do.To view W.B.C.S. Mathematics Optional Syllabus , Click here.

The last two coordinate pairs use the fact that if we end up in the opposite quadrant from the point we can use a negative $r$ to get back to the point and of course there is both a counter clock-wise and a clock-wise rotation to get to the angle.

These four points only represent the coordinates of the point without rotating around the system more than once. If we allow the angle to make as many complete rotations about the axis system as we want then there are an infinite number of coordinates for the same point. In fact, the point $\left(r,\theta \right)$ can be represented by any of the following coordinate pairs.

$$\left(r,\theta +2\pi n\right)\left(-r,\theta +\left(2n+1\right)\pi \right),\text{where}n\text{is any integer}\text{.}$$

Next, we should talk about the origin of the coordinate system. In polar coordinates the origin is often called the pole. Because we aren’t actually moving away from the origin/pole we know that $r=0$. However, we can still rotate around the system by any angle we want and so the coordinates of the origin/pole are $\left(0,\theta \right)$.

Now that we’ve got a grasp on polar coordinates we need to think about converting between the two coordinate systems. Well start out with the following sketch reminding us how both coordinate systems work.

Note that we’ve got a right triangle above and with that we can get the following equations that will convert polar coordinates into Cartesian coordinates.

Please subscribe here to get all future updates on this post/page/category/website

Want to keep yourself updated about WBCS and other Govt. exams? Submit the form here-

For all WBCS Exam etc. course details CLICK HERE

If you want to be in contact with us and get future posts and news, subscribe here...

* indicates required

Email Address *

First Name

Your information will *never* be shared or sold to a 3rd party.