Merchant Force Diagram - Mechanical Engineering

Posted on October 1st, 2019 in Mechanical Engineering
Tags: Mechanical Engineering, Notes, WBCS

Merchant Force Diagram – Mechanical Engineering Notes – For W.B.C.S. Examination.

মার্চেন্ট ফোর্স ডায়াগ্রাম – মেকানিকাল ইঞ্জিনিয়ারিং নোট – WBCS পরীক্ষা।

Orthogonal Cutting – assumes that the cutting edge of the tool is set in a position that is perpendicular to the direction of relative work or tool motion. This allows us to deal with forces that act only in one plane.Continue Reading Merchant Force Diagram – Mechanical Engineering Notes – For W.B.C.S. Examination.

We can obtain orthogonal cutting by turning a thin walled tube, and setting the lath bit cutting edge perpendicular to the tube axis.

Next, we can begin to consider cutting forces, chip thicknesses, etc.

First, consider the physical geometry of cutting,

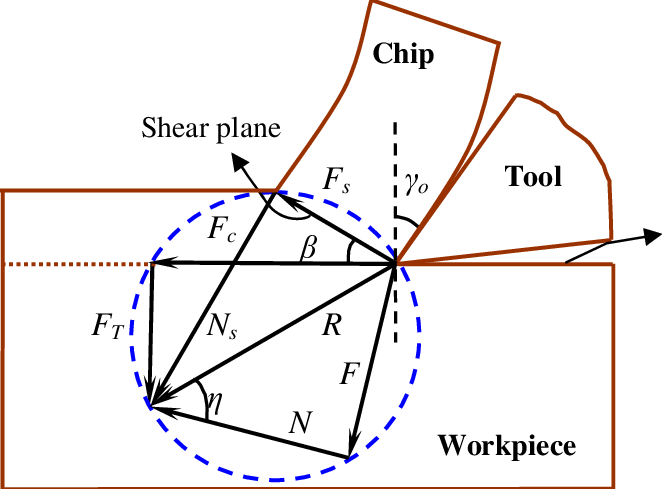
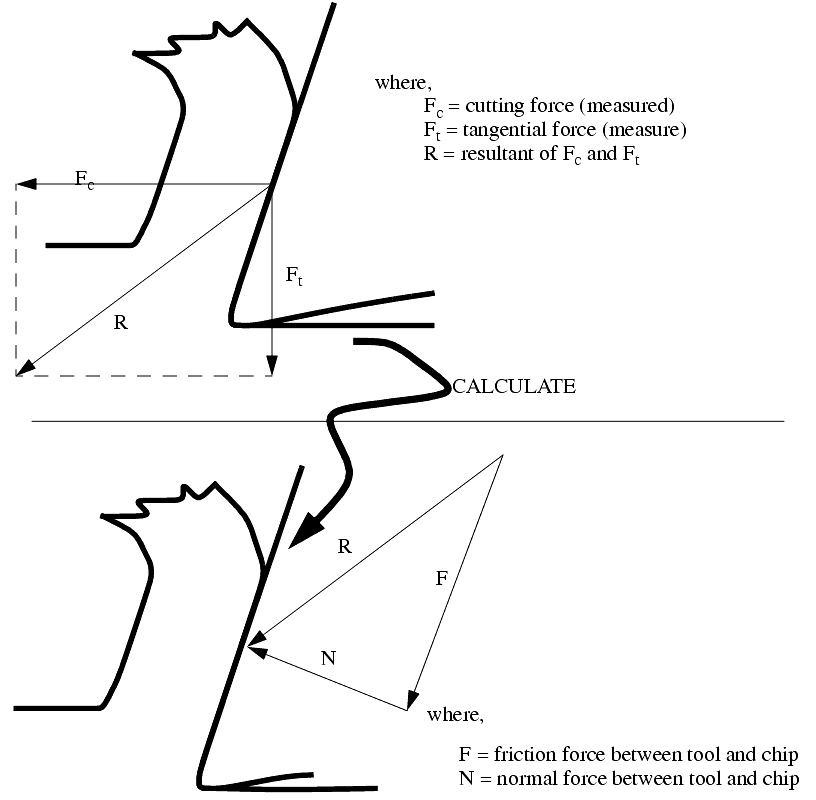
Next, we assume that we are also measuring two perpendicular cutting forces that are horizontal, and perpendicular to the figure above. This then allows us to examine specific forces involved with the cutting. The cutting forces in the figure below (Fc and Ft) are measured using a tool force dynamometer mounted on the lathe.

Merchant’s Force Circle is a method for calculating the various forces involved in the cutting process. This will first be explained with vector diagrams, these in turn will be followed by a few formulas.

The procedure to construct a merchants force circle diagram (using drafting techniques/instruments) is,

1. Set up x-y axis labeled with forces, and the origin in the centre of the page. The scale should be enough to include both the measured forces. The cutting force (Fc) is drawn horizontally, and the tangential force (Ft) is drawn vertically. (These forces will all be in the lower left hand quadrant) (Note: square graph paper and equal x & y scales are essential)

2. Draw in the resultant (R) of Fc and Ft.

3. Locate the centre of R, and draw a circle that encloses vector R. If done correctly, the heads and tails of all 3 vectors will lie on this circle.

4. Draw in the cutting tool in the upper right hand quadrant, taking care to draw the correct rake angle (a) from the vertical axis.

5. Extend the line that is the cutting face of the tool (at the same rake angle) through the circle. This now gives the friction vector (F).

6. A line can now be drawn from the head of the friction vector, to the head of the resultant vector (R). This gives the normal vector (N). Also add a friction angle (t) between vectors R and N. As a side note recall that any vector can be broken down into components. Therefore, mathematically, R = Fc + Ft = F + N.

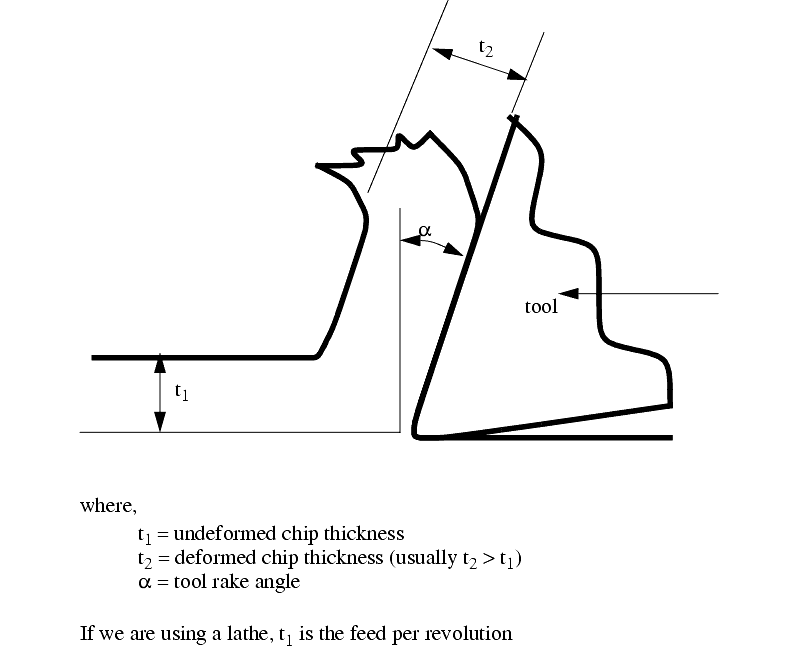
7. We next use the chip thickness, compared to the cut depth to find the shear force. To do this, the chip is drawn on before and after cut. Before drawing, select some magnification factor (e.g., 200 times) to multiply both values by. Draw a feed thickness line (t1) parallel to the horizontal axis. Next draw a chip thickness line parallel to the tool cutting face.

8. Draw a vector from the origin (tool point) towards the intersection of the two chip lines, stopping at the circle. The result will be a shear force vector (Fs). Also measure the shear force angle between Fs and Fc.

9. Finally add the shear force normal (Fn) from the head of Fs to the head of R.

10. Use a scale and protractor to measure off all distances (forces) and angles.

Our own publications are available at our webstore (click here).

For Guidance of WBCS (Exe.) Etc. Preliminary , Main Exam and Interview, Study Mat, Mock Test, Guided by WBCS Gr A Officers , Online and Classroom, Call 9674493673, or mail us at – mailus@wbcsmadeeasy.in
Visit our you tube channel WBCSMadeEasy™ You tube Channel
Please subscribe here to get all future updates on this post/page/category/website

Recent updates

Tags

Merchant Force Diagram – Mechanical Engineering Notes – For W.B.C.S. Examination.

মার্চেন্ট ফোর্স ডায়াগ্রাম – মেকানিকাল ইঞ্জিনিয়ারিং নোট – WBCS পরীক্ষা।

Leave a Reply Cancel reply