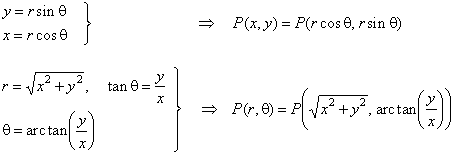Polar To Cartesian Conversion Formulas – Mathematics Notes – For W.B.C.S. Examination.

There are many rules regarding what optional subject to choose for the W.B.C.S.  exam. A general rule of thumb is that you should take the subject in which you have some background and a genuine interest and practice till you are perfect.. In case you are a mathematics graduate and enjoy learning this subject, choosing maths as your W.B.C.S.optional might be a good idea. Mathematics is one of the most scoring optional in the W.B.C.S. Mains examination. The aspirants from B. Sc Mathematics or B. Tech background can take Mathematics as the optional in this examination.  Learning Mathematics is always fun. Right strategy and thorough practice is the key to crack Mathematics optional.Converting from Cartesian is almost as easy. Let’s first notice the following.Continue Reading Polar To Cartesian Conversion Formulas – Mathematics Notes – For W.B.C.S. Examination.

$$\begin{array}{cc}{x}^2+y^2& ={\left(r\cos \theta \right)}^2+{\left(r\sin \theta \right)}^2\\ & =r^2{\cos }^2\theta +r^2{\sin }^2\theta \\ & =r^2\left({\cos }^2\theta +{\sin }^2\theta \right)=r^2\end{array}$$

This is a very useful formula that we should remember, however we are after an equation for $r$ so let’s take the square root of both sides. This gives,

$$r=\sqrt{x^2+y^2}$$

Note that technically we should have a plus or minus in front of the root since we know that $r$ can be either positive or negative. We will run with the convention of positive $r$ here.

Getting an equation for $\theta$ is almost as simple. We’ll start with,

$$\frac{y}{x}=\frac{r\sin \theta }{r\cos \theta }=\tan \theta$$

Taking the inverse tangent of both sides gives,

$$\theta ={\tan }^{-1}\left(\frac{y}{x}\right)$$

We will need to be careful with this because inverse tangents only return values in the range $-\frac{\pi }{2}<\theta <\frac{\pi }{2}$. Recall that there is a second possible angle and that the second angle is given by $\theta +\pi$.

Summarizing then gives the following formulas for converting from Cartesian coordinates to polar coordinates.

The equation given in the second part is actually a fairly well known graph; it just isn’t in a form that most people will quickly recognize. To identify it let’s take the Cartesian coordinate equation and do a little rearranging.

$$x^2+8x+y^2=0$$

Now, complete the square on the $x$ portion of the equation.

$$\begin{array}{cc}{x}^2+8x+16+y^2& =16\\ {\left(x+4\right)}^2+y^2& =16\end{array}$$

So, this was a circle of radius 4 and center $\left(-4,0\right)$.

This leads us into the final topic of this section.

Common Polar Coordinate Graphs

Let’s identify a few of the more common graphs in polar coordinates. We’ll also take a look at a couple of special polar graphs.

Lines
Some lines have fairly simple equations in polar coordinates.To view W.B.C.S. Mathematics Optional Syllabus , Click here.

1. $\theta =\beta$.
   We can see that this is a line by converting to Cartesian coordinates as follows$$\begin{array}{cc}\theta & =\beta \\ {\tan }^{-1}\left(\frac{y}{x}\right)& =\beta \\ \frac{y}{x}& =\tan \beta \\ y& =\left(\tan \beta \right)x\end{array}$$This is a line that goes through the origin and makes an angle of $\beta$ with the positive $x$-axis. Or, in other words it is a line through the origin with slope of $\tan \beta$.
2. $r\cos \theta =a$
   This is easy enough to convert to Cartesian coordinates to $x=a$. So, this is a vertical line.
3. $r\sin \theta =b$
   Likewise, this converts to $y=b$ and so is a horizontal line.

Please subscribe here to get all future updates on this post/page/category/website

Want to keep yourself updated about WBCS and other Govt. exams? Submit the form here-

For all WBCS Exam etc. course details CLICK HERE

If you want to be in contact with us and get future posts and news, subscribe here...

* indicates required

Email Address *

First Name

Your information will *never* be shared or sold to a 3rd party.